属性

并查集的逻辑结构是一个包含N个元素的集合，如图：

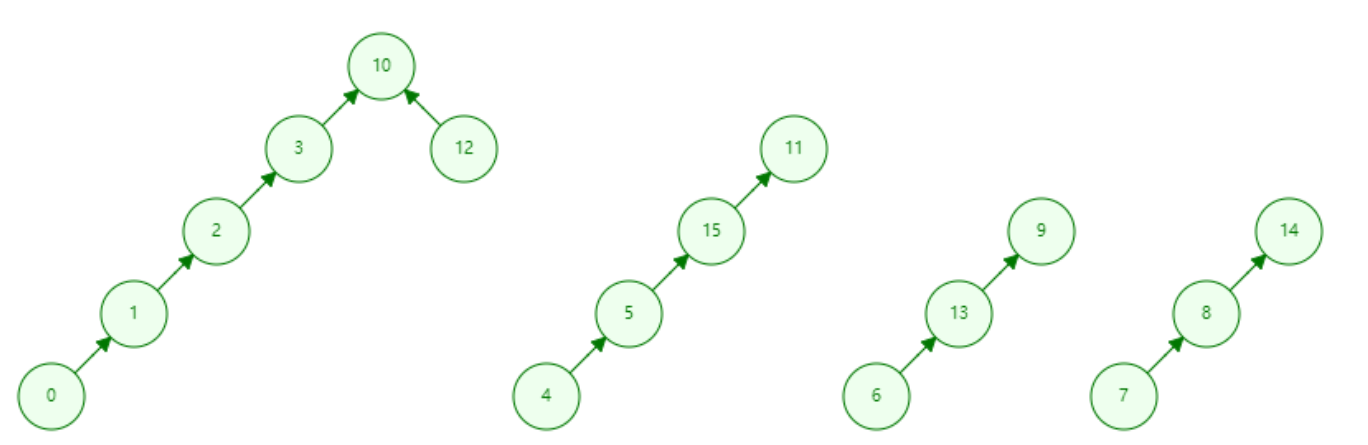
并查集的存储结构是一个包含N个元素的树，如图：

用一个数组存储p[x]来存储每个元素（点）的父节点

讲解知识点

基本原理

每个集合的根节点便是这个集合的编号，每个点存储自己的父节点(初始化)

1
2
3
4
for(int i=1;i<=n;i++)
{
    p[i]=i;
}

树根：p[x]==x //(父节点等于自己)

求集合编号：while(p[x]!=x) x=p[x] //(不是根节点的话，置换成父节点进行再次判断)

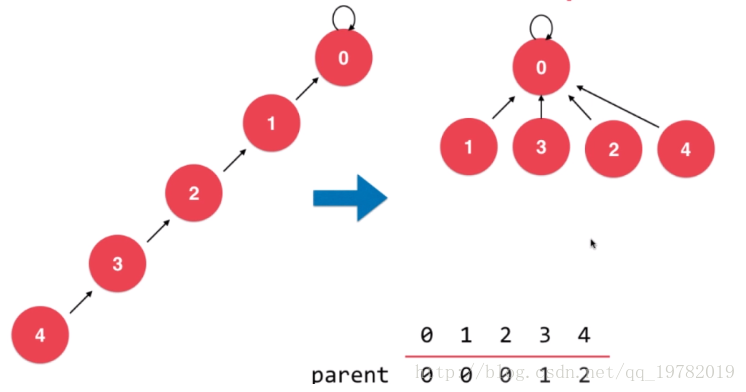
路径压缩优化
1
2
3
4
5
6
7
8
int find(int x)//找根节点
{
    if (p[x]!=x)//父节点等于自己的是根节点
    {
        p[x] = find(p[x]);//递归到根节点
    }
    return p[x];
}

并查集的两种基本操作
1.将两个集合合并

p[find(a)] = find(b)

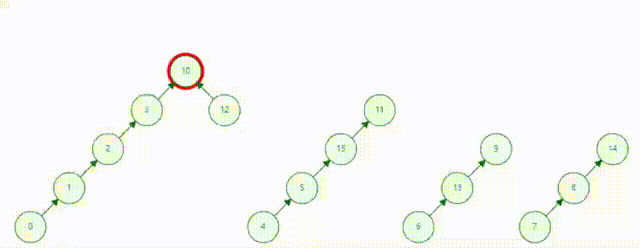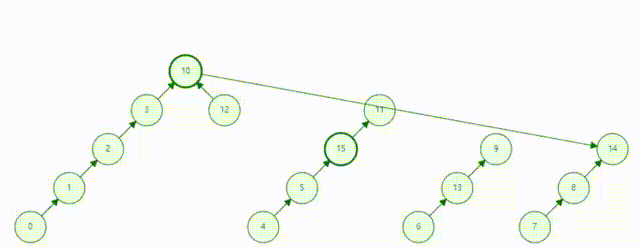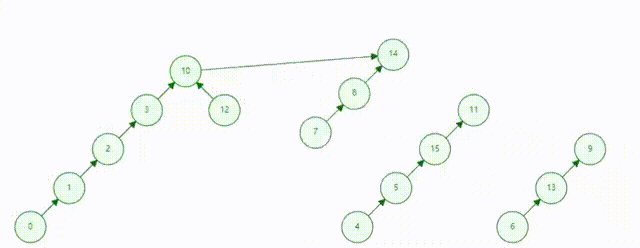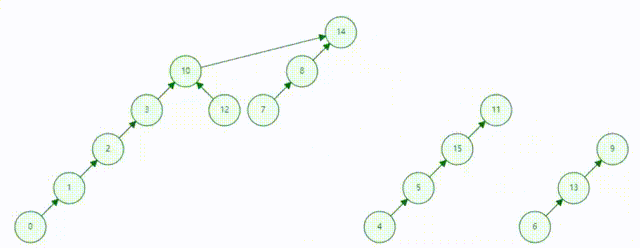
2.询问两个集合是否在同一集合

if (find(a) == find(b))

例题

https://www.luogu.com.cn/problem/P3367

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;
const int N=10010;
int p[N];
int find(int x)//找根节点函数 
{
	if(p[x]!=x)
	{
		p[x]=find(p[x]);//递归去找根节点
	}
	return p[x];
}
int main() {
	
	int n,m;
	cin>>n>>m;
	//初始化 ，是每个元素是一个集合 
	for(int i=1;i<=n;i++)
	{
		p[i]=i;
	}
	while(m--)
	{
		int z,x,y;
		cin>>z>>x>>y;
		if(z==1)
		{
			p[find(x)]=find(y);//合并集合
		}	
		else
		{
			if(find(x)==find(y))//判断是否属于同一集合
			{
				cout<<"Y"<<endl;
			}
			else
			{
				cout<<"N"<<endl;
			}
		}
	}
	return 0;
}